My research interests are in the development, analysis, and application of numerical methods used in the simulation of various physical processes such as Fluid Dynamics, Heat and Mass Transfer, Phase Change, and Wave propagation. I am also interested in the numerical solution of Partial Differential Equations. Lately, I got interested in the level set method with its applications such as image segmentation, distance function calculation, fast marching methods, ... . Below you will find some of the topics I have been working on.
Adapative mesh refinement
| The numerical simulation of physical processes with large localized gradients requires a very fine mesh. One way to minimize computational resources consist in refining the grid localy. We have developed a program that refines and coarsens the grid dynmically as the solution evolves with time. The initial triangular unstructured grid, which is not necessarily uniform, is modified via an algorithm which is based on a quadtree structure where each refined triangle is subdivided into four smaller triangles. Several levels of refinement may be achieved. |
 Animation (*.avi, 23MB) |
Phase change with convection
| The gallium melting problem (Gau and Viskanta 1986) is a model problem for testing codes designed for the numerical simulation of Phase change problems with convection. We have developped an-enthalpy-formulation based code for solving the two-dimensional Navier-Stokes equations of a pure solid undergoing melting. The picture on the right shows our restulst for the evolution of the solid-liquide interface with time contrasted to the results of Brent and Voller (1988). Although these results are in quite good agreement with the experimental results, they have proven to be wrong! See below. |
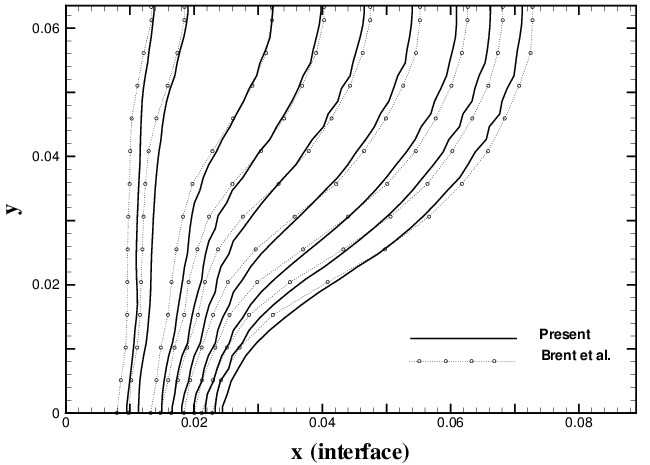 |
Reference solution for Phase change with convection
A numerical study we have performed has shown that very fine grids are required in order to capture the correct roll structure in the flow (4 then 3 then 2 rolls). As a result, the actual interface (see below) shows more bumps than in the picture above. The figure below shows the roll structure as well as liquid-solid interface for the gallium melting problems at several times.




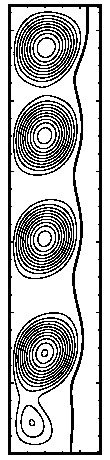
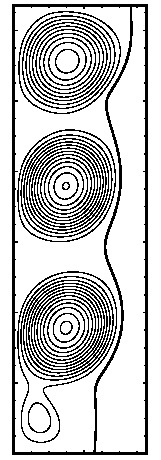
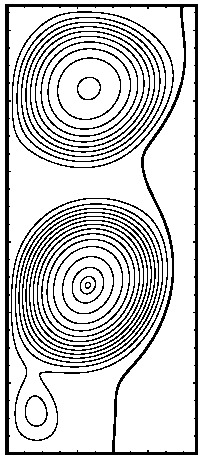
Solid-liquide interface and streamlines for gallium melting
problem at times 20, 32, 36, 42, 85, 155 and 280 seconds.
Spectral Difference Method
| The Spectral Difference Method is a new higher order method that was introduced by Z.J. Wang and coworkers for the solution of PDEs and in particular conservation laws (Extension to the Navier-Stokes equations in 2007). As part of their thesis for the degree of State Engineer in Mechanics (in June 2008), Takfarines Ait-Ali and Fateh Boukria undertook the difficult task of writing a twodimensional compressible Navier-Stokes solver based on the Spectral Difference Method. It took them four months to get the code to work, two weeks before the deadline. One of their results shown on the right is about the flow around an NACA0012 airfoil for a Mach number M=0.5, Reynolds number Re=5000, and angle of attack α=0. |
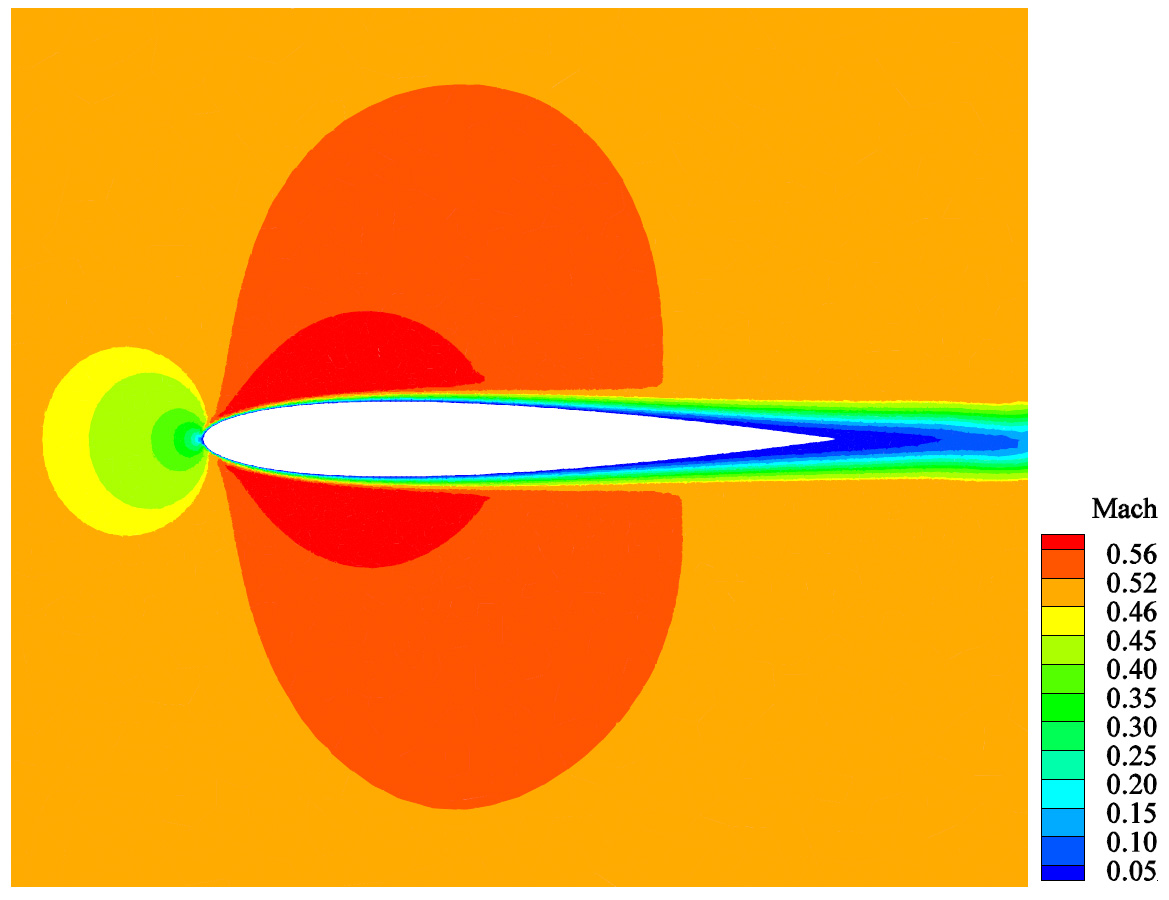 Mach number contours around NACA0012 airfoil
|
Hybrid mesh generation
Unstructured grids are almost indispensable for the simulation of real world problems. For complex shaped domains, the grid is usually not adequate near the interface (see the circle on the figure) due to the presence of a boundary layer. In such cases, a body-fitted structured grid is best suited near the interface. A part of his Masters' thesis (June 2010), Abdelkhalek Balehouane undertook the task of writing a program that gerenates a hybrid mesh for a given geometry. Given the geometry of the domain, they implemented a new method "Characterisitc Fast Marching" for the calculation of the distance function (E. Cristiani 2008) and used it to generate the body-fitted grid around the inner circle (figure below, left). Then, they used the grid generator developed by Smail Khalfallah and Khalid Mechalikh to gerenate the outside unstructured grid. The resulting hybrid mesh is shown in the figure.
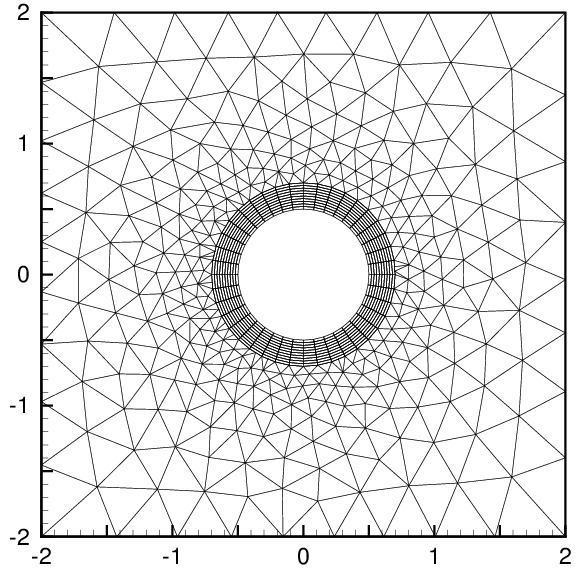
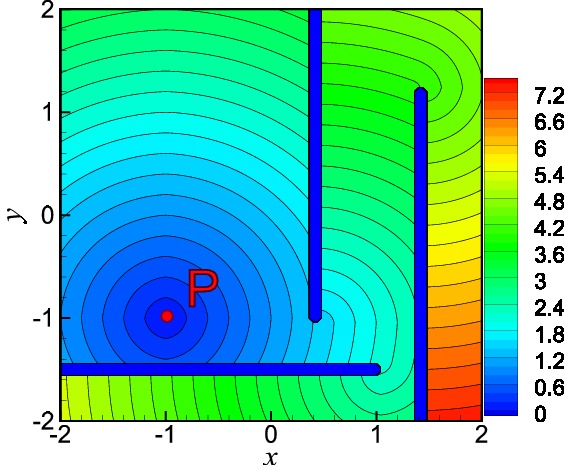
Hybrid mesh for domain with circular hole (left) and contours of distance
function to the point P for a domain with obstacles (right)
Linear system solvers
Choosing apropriate solvers for large and sparse linear systems is not a trivial task. In particular, the efficiency of a given solver often depends on the properties of the system coefficient matrix. We performed a comparison for a selection of sparse linear systems solvers and preconditioners on a real application: linear systems that result from the discretization by the finite volumes method of a model for phase change plus convection. The model is based on an enthalpy formulation in conjunction with the incompressible Navier-Stokes equations. The figures below show the evolution of the residual as a function of the number of iterations for a solver-preconditioner selected set.
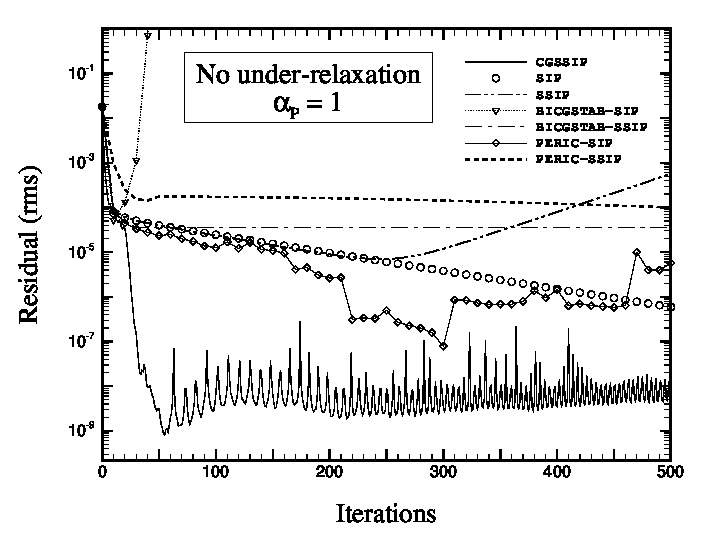
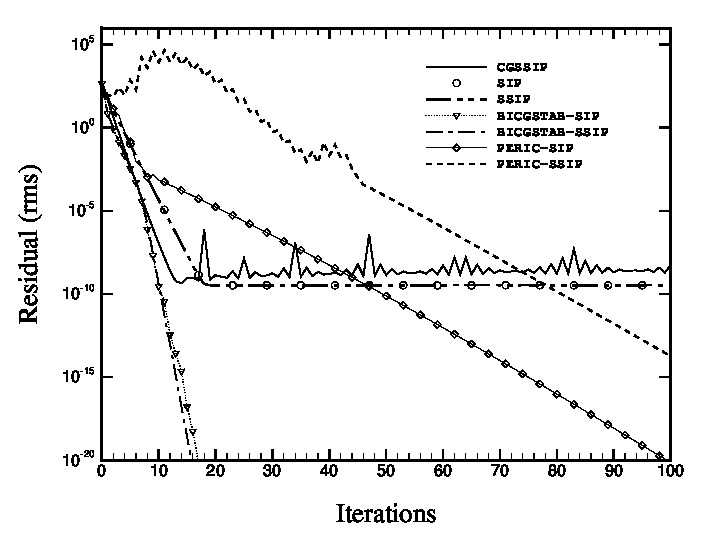
SDP linear system from pressure equation (left) and non-symmetric linear system
from energy equation (right)
Outflow boundary conditions
Boundary conditions are paramount to the success of any numerical simulation. Indeed, since many different physcial problems are governed by the same mathematical model, the difference in the solution will only come from the choice of boundary conditions. It is well known that the computational domain has to be limited, thus introducing fictitious boundaries where appropriate boundary conditions need to be specified. At and ouflow, care must be take in order to avoid the reflection of spurious waves. Typically, one has to resort to the use of so-called non-reflecting boundary conditions. We implemented the NSCBC boundary condition developped by Poinsot and Lele in a compresible Navier-Stokes solver and tested it on the problem of the entropy wave advected by a uniform flwo. The figure below shows the entropy contours at three different times.

Entropy wave crossing the outflow boundary
Software
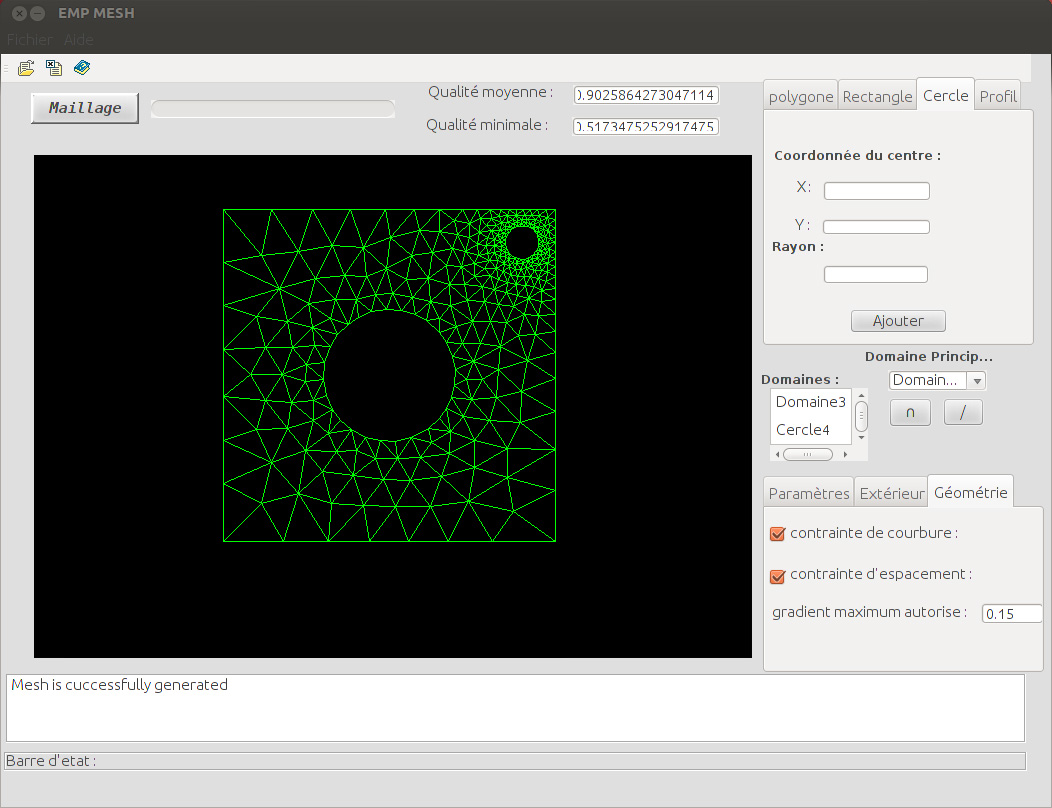
- EMPMesh - A two-dimensional unstructured grid generator for arbitrary geometries (See interface below). Written in Java by Smail Khalfallah and Khalid Mechalikh (Enginneer Thesis 2006). The software has been updated several times by S. Khalfallah and was ported to both Windows and Linux (2012 latest version). Thanx to this software, the students in my Finite Element Class were able to generate a grid for solving various problems with complex geometries.